Simple and best practice solution for y=x/31 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,MATH FINDING THE DOMAIN OF A FUNCTION KSU Deflnitions † Function A function f is a rule that assigns to each element x in the set A exactly one element, called f(x), in the set BThe set A is called the domain and the set B is called the range † Domain The domain of a function is the set of all real numbers for which the expression is deflned as a real numberExample is y = x 2 symmetric about the yaxis?
Linear Relationship Rules Passy S World Of Mathematics
Y=3(x-1)^2+2 in standard form
Y=3(x-1)^2+2 in standard form-Algebra Graph y=x^ (1/3) y = x1 3 y = x 1 3 Graph y = x1 3 y = x 1 333 Version 3 Answers 1 Differentiate the function f (x) = log10 (x^3 4) 2 Differentiate the function f (x) = 9x ln (6x) – 9x 3 Differentiate the function f (x) = sin (7 ln x) 4 Differentiate the function f (x) = ln (121 sin^2x)




Ppt Rate Of Change And Slope Powerpoint Presentation Free Download Id
Explanation Using synthetic division and the fact that x = − 1 is obviously a solution we find that we can expand this to (x 1)(x2 −x 1) = 0 In order to have LHS=RHS need one of the brackets to be equal to zero, ie (x 1) = 0 1 (x2 − x 1) = 0 2 From 1 we note that xY=x3x212x No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation y(x^3x^212*x)=0The algorithm will be improved If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below Your input find the area between the following curves $$$ y = x^ {2} $$$ , $$$ y = \sqrt {x}
Inverse Functions An inverse function goes the other way!Using https//wwwwolframalphacom/ tangent line to y=x^2 through (3,1) tangent line to y=x^2 through (3,1) WolframAlpha gives a result of note Wolfram didn'tA short cut for implicit differentiation is using the partial derivative (∂/∂x) When you use the partial derivative, you treat all the variables, except the one you are differentiating with respect to, like a constant For example ∂/∂x 2xy y^2 = 2y In this case, y is treated as a constant Here is another example ∂/∂y 2xy
An online derivative calculator that differentiates a given function with respect to a given variable by using analytical differentiation A useful mathematical differentiation calculator to simplify the functions Just copy and paste the below code to your webpage where youAspect ratio Values One to one or Golden ratio or # # Default One to one The Aspect ratio option controls the ratio of the height of the plot to its width When One to one is checked the ratio is 11 and the scales on the two axes will be identical This will ensure that circles, for example, will actually appear circular on the screen When Golden ratio is selected, the aspect ratio isMath 334 Assignment 1 — Solutions 6 Solution We look for an integrating factor of the form µ = µ(xy) Multplying through by µ gives µ(xy)M(x,y)dxµ(xy)N(x,y)dy = 0,




Solve The Initial Value Problem Y X 3 1 Y Chegg Com



Modulus Function
How to Check Your Answer with Algebra Calculator First go to the Algebra Calculator main page Type the following First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6Question how do you graph y=1/2x 3 Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website! Get an answer for 'Find the inverse function of f(x)=x^32?' and find homework help for other Math questions at eNotes



Graph Graph Equations With Step By Step Math Problem Solver




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In
we know that The equation of the given line in the graph is The given line is parallel to the xaxis so the perpendicular line to the given line will be parallel to the yaxis and the equation will be equal to the xcoordinate of the given pointThe method of differentiating functions by first taking logarithms and then differentiating is called logarithmic differentiation We use logarithmic differentiation in situations where it is easier to differentiate the logarithm of a function than to differentiate the function itself This approach allows calculating derivatives of power, rational and some irrational functions in an efficientFree functions inverse calculator find functions inverse stepbystep



Quadratic Graphs Including Parabolas Sketching Related Graphs And Relationship To Factors



Graph The Linear Equation Yx 2 1 Draw
Let us start with an example Here we have the function f(x) = 2x3, written as a flow diagram The Inverse Function goes the other way So the inverse of 2x3 is (y3)/2Figure 1 The volume of the solid formed by revolving the region bounded by the curve y = f (x) and the x− axis between x = a and x = b about the x− axis is given by V = π b ∫ a f (x)2dx The cross section perpendicular to the axis of revolution has the form of a disk of radius R = f (x) Similarly, we can find the volume of the solidSection 1 Introduction 4 Example 1 Consider the equation y = xnThis is a power curve, but if we take the logarithm of each side we obtain log(y) = log(xn) = nlog(x) since log(xn) = nlog(x) If Y = log(y) and X = log(x) then Y = nX




Ppt Rate Of Change And Slope Powerpoint Presentation Free Download Id




If X 3 Y 3 1 And X 4 Y 4 1 What Is The Value Of X And Y Quora
I'm a college sophomore student and I am taking a Business Calculus class And I'm having a REALLY hard time trying to figure out this problem If f ' (x) = 3x^2 1, find the equation of the tangent line to f(x) = x^3 x at x= 1$\begingroup$ Your answer and another comment made above made it clear I was wrong in attempting to use the derivative of the function as the slope of the tangent That was my mistake How silly However, while I can see how I'd get the slope and use it, and that your equation y2 = 3(x1) does become y = 3x1 (The slope)Try to replace x with − x y = (−x) 2 Since (−x) 2 = x 2 (multiplying a negative times a neagtive gives a positive), there is no change So y = x 2 is symmetric about the yaxis



Draw The Graph Of The Equation 2 X 3 3 1 Y 0 Also Find The Point Where The Line Meets X Axis Mathematics Topperlearning Com 9107



Assignment 1
Hi Kilihea, The slopeintercept form of a line is y = mx b If you write an equation in this form then m is the slope and b is the yintercept This is an extremely useful form if you are to sketch the graph since b tells you a point on the curve (0, b) and mTherefore, the closer b is to r, the better an approximation f(b)/(b r) is to the derivative f (1) (r), and therefore, the faster the convergence To visualize this, suppose the right end point b is fixed and the other, a, is sufficiently close to the root that the function f(x) is closely approximated by the Taylor series, that is, f(a) ≈ f (1) (r)(a r)When x = 1, y = –x – 3 = –(1) – 3 = –4 Then the solution consists of the points (–4, 1) and (1, –4) Note the procedure I solved one of the equations (the first equation looked easier) for one of the variables (solving for " y =" looked easier ), and then plugged the




Given Z F X Y X X U V Y Y U V With X 5 2 3 Y 5 2 1 Calculate Z U 5 2 In Terms Of Some Of The Values Given In The Table Below F X 5 2 A F Y 5 2 2 X U 5 2



Quadratics Graphing Parabolas Sparknotes
Please Subscribe here, thank you!!!Answer by funmath (2933) ( Show Source ) You can put this solution on YOUR website!Looking at we can see that the equation is in slopeintercept form where the slope is and the yintercept is Since this tells us that the yintercept is Remember the yintercept is the point where the



How Do You Graph Y X 3 1 Socratic
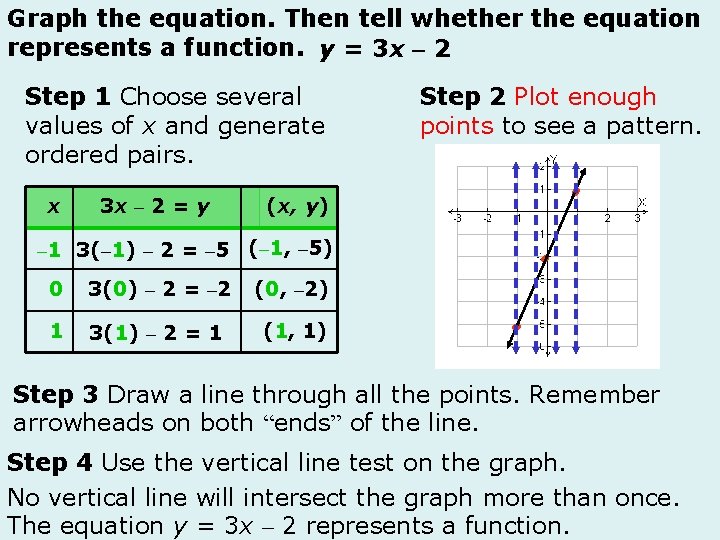



Graph The Linear Equation Yx 2 1 Draw
Correct answer \displaystyle y=4x2 Explanation First, find the slope of this tangent line by taking the derivative \displaystyle y' = 6x 2 Plugging in 1 for x \displaystyle 6 (1)2 = 62 = 4 So the slope is 4 Now we need to find the ycoordinate when x is 1, so plug 1 in to the original equationSOLUTION 1 Begin with x3 y3 = 4 Differentiate both sides of the equation, getting (Remember to use the chain rule on D ( y3 ) ) so that (Now solve for y ' ) Click HERE to return to the list of problems SOLUTION 2 Begin with ( x y) 2 = x y 1 Differentiate bothHow to solve and grah this equation y=x^3 1 If x=2 y= (2)^31 y=81 y=7 Plot (2,7) If x=1 y= (1)^31



File Y X 3 3x 1 Svg Wikimedia Commons




Solve The Initial Value Problem Dy Dx Y 1 X 3 Chegg Com
Question from Princess, a student Hi!The pointslope form of a line with slope m and passing through the point (x 1, y 1 ) is y y 1 m (x x 1) The slopeintercept form of a line with slope m and yintercept b is y = mx b A relationship determined by an equation of the form y = kx (k a constant) is called a direct variationSimply look for a constant increase in y after plugging in values for x, or graph the equation and look for a straight line A linear equation will have constantly increasing y values and a straight line, while a nonlinear equation will have outputs increasing at a nonconstant rate and a curved graph After awhile, determining these functions




Cartesian Coordinate System Wikipedia
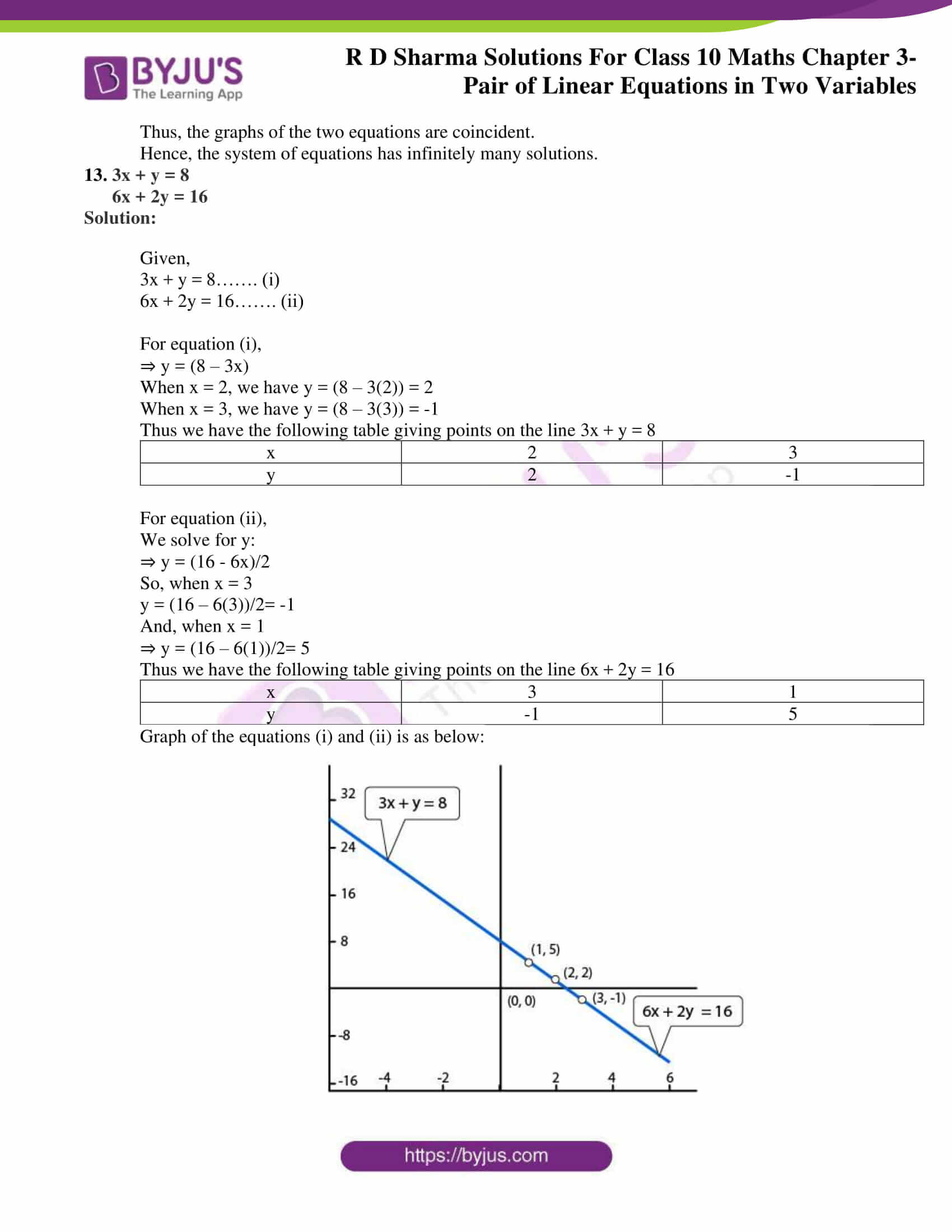



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
Graph y=x^31 y = x3 − 1 y = x 3 1 Find the point at x = −2 x = 2 Tap for more steps Replace the variable x x with − 2 2 in the expression f ( − 2) = ( − 2) 3 − 1 f ( 2) = ( 2) 3 1 Simplify the result Tap for more steps Raise − 2 2 to the power of 3 3According to Theorem 4 of Lesson 2 The rate of change of f(x) is 2 for all values of xf '(x) is constantBut that should be obvious y = 2x − 5 is the equation of a straight line whose slope is 2 (Topic 9 of Precalculus)And the value of the slope of a straight line is the rate of change of y with respect to x so many units of y for each unit of xNext I'll turn to the issue of horizontal or slant asymptotes Since the degrees of the numerator and the denominator are the same (each being 2), then this rational has a nonzero (that is, a nonxaxis) horizontal asymptote, and does not have a slant asymptoteThe horizontal asymptote is found by dividing the leading terms




Area Of A Region Bounded By Y 8 And Y X 2 1 Mathematics Stack Exchange




Rebyat Postrojte Grafik Funkcii Y X3 1 Po Grafiku Najdite A Znachenie Funkcii Pri Znachenii Shkolnye Znaniya Com
Solution To factor the above trinomial, we need to write it in the form 9x 2 3x 2 = (ax m) (bx n) Expand the product on the right above 9x 2 3x 2 = abx 2 x (mb na) mn For the polynomial on the left to be equal to the polynomial on the right we need to have equal corresponding coefficients, hence ab = 9Graph each function y=x^{3}1 Boost your resume with certification as an expert in up to 15 unique STEM subjects this summerY= ((x^3) 1)^4 * ((x^4)1)^3 Best Answer This is the best answer based on feedback and ratings dy/dx =




3 1 Systems Of Linear Equations 3




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyExplanation Convert the equation to slope intercept form to get y = –1/3x 2 The old slope is –1/3 and the new slope is 3 Perpendicular slopes must be opposite reciprocals of each other m 1 * m 2 = –1 With the new slope, use the slope intercept form and the point to calculate the intercept y = mx b or 5 = 3(1) b, so b = 2 So y = 3x 2 Find the volume if the area bounded by the curve `y = x^3 1`, the `x`axis and the limits of `x = 0` and `x = 3` is rotated around the `x`axis Answer This is the region as described, under a cubic curve 1 2 31 5 10 15 25 30 x y Open image in a new page




Ex 6 3 3 Find Slope Of Tangent Y X3 X 1 At X 2



Quadratics Graphing Parabolas Sparknotes
Parallel lines are a fixed distance apart and will never meet, no matter how long they are extended Lines that are parallel have the same gradient The graphs above, \(y = 2x 1\) and \(y = 2x2xy=1 Geometric figure Straight Line Slope = 2 xintercept = 1/2 = yintercept = 1/1 = Rearrange Rearrange the equation by subtracting what is to the right of theThe natural logarithm can be defined in several equivalent ways The natural logarithm of a positive, real number a may be defined as the area under the graph of the hyperbola with equation y = 1/x between x = 1 and x = aThis is the integral = If a is less than 1, then this area is considered to be negative This function is a logarithm because it satisfies the fundamental



How Do You Graph The Function Y X 3 Socratic




Otvety Mail Ru Grafik Funkcii Y X 3 1 V Kakih Chetvertyah Lezhit Dannyh Grafik
The root (1 i √3)/2 is denoted by ω Hence the roots of x^3 = 1 are 1, ω, ω^2 These three roots of x^3=1 are called the cube roots of unity We also observe that 1 ωω^2 = 0 and ω^3 = 1 Help develop an app that can assess vitiligo treatment efficacyGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




What Does The Graph Of Math X 3 Y 3 Z 3 1 Math Look Like Quora




Find The Area Bounded By Curves Y X 2y 3 X And X Axis



Assignment 1
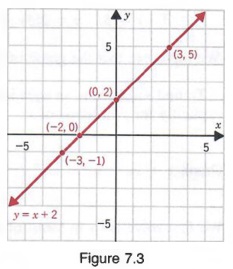



Graph Graph Equations With Step By Step Math Problem Solver



How Do We Graph The Equation X 2 Y 3 1 What Is The Slope Quora



How Do You Graph Y X 3 Example




1 Postrojte Grafik Funkcii Y X 3 V Kube 1 Po Grafiku Najdite A Znachenie Funkcii Pri Shkolnye Znaniya Com



2




Graph Of Y X 3 Novocom Top




Ppt Warm Up Evaluate Each Expression For X 1 And Y 3 1 X 4 Y 2 2 X Y Powerpoint Presentation Id




Answered 3 3 Increasing And Decreasing Functions Bartleby



X3 Px Q 0




If X 3 1 Y 2 3 5 3 1 3 Find The Values Of X And Y




Graphing X 3 2 Y 3 2 1 Mathematics Stack Exchange




The Equation Of The Quadratic Function Represented By The Graph Is Y A X 3 2 1 What Is The Value Of Brainly Com



Y 1 X




How Do You Find The Volume Bounded By Y X 3 Y X And Y 1 Revolved About The X 1 Socratic
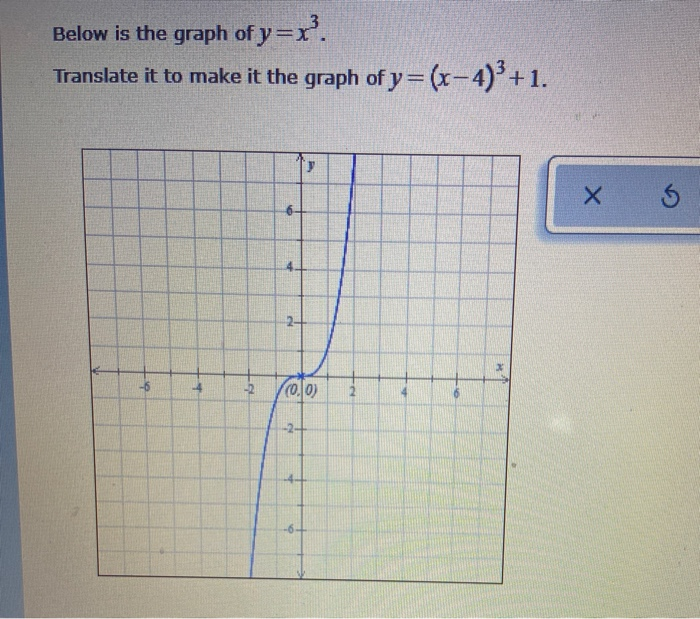



Below Is The Graph Of Y X Translate It To Make It Chegg Com



Linear Relationship Rules Passy S World Of Mathematics
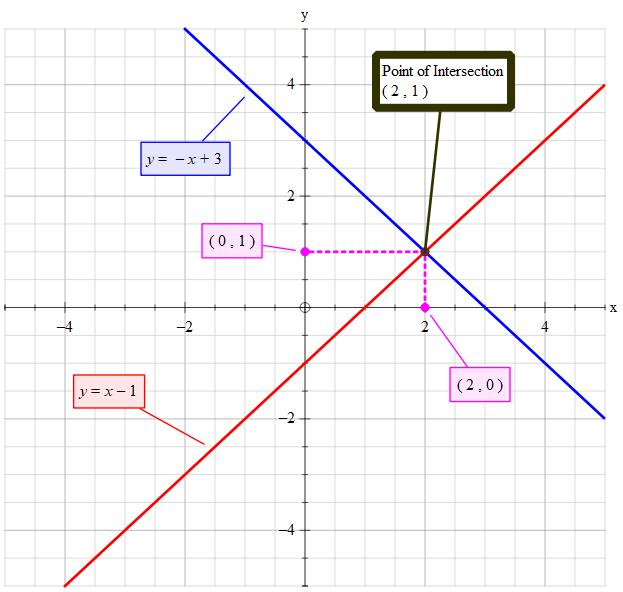



How Do You Solve The System Of Equations X Y 3 X Y 1 By Graphing Socratic



Solution How To Solve And Grah This Equation Y X3 1




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube



Graph Graph Equations With Step By Step Math Problem Solver
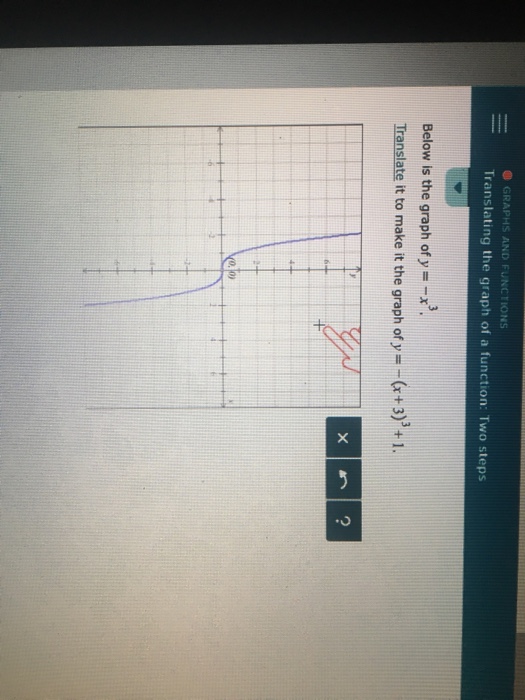



Below Is The Graph Of Y X 3 Translate It To Make Chegg Com




Solving Systems Of Linear Equations Glencoe




5 5 Parallel Perp Lines




Find The Equations Of All Lines Having Slope 0 Which Are Tangent To The Curve Y 1x 2 2x 3
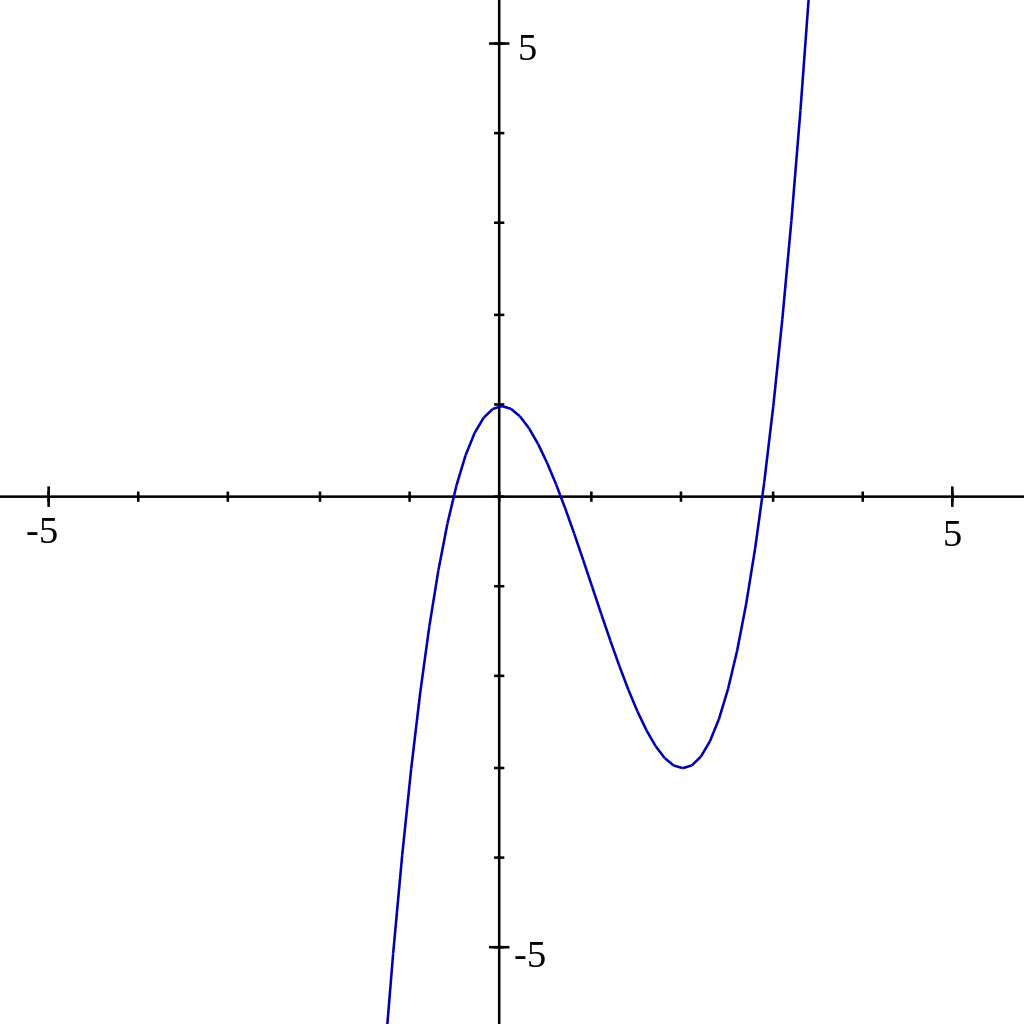



File Y X 3 3x 2 1 Svg Wikimedia Commons
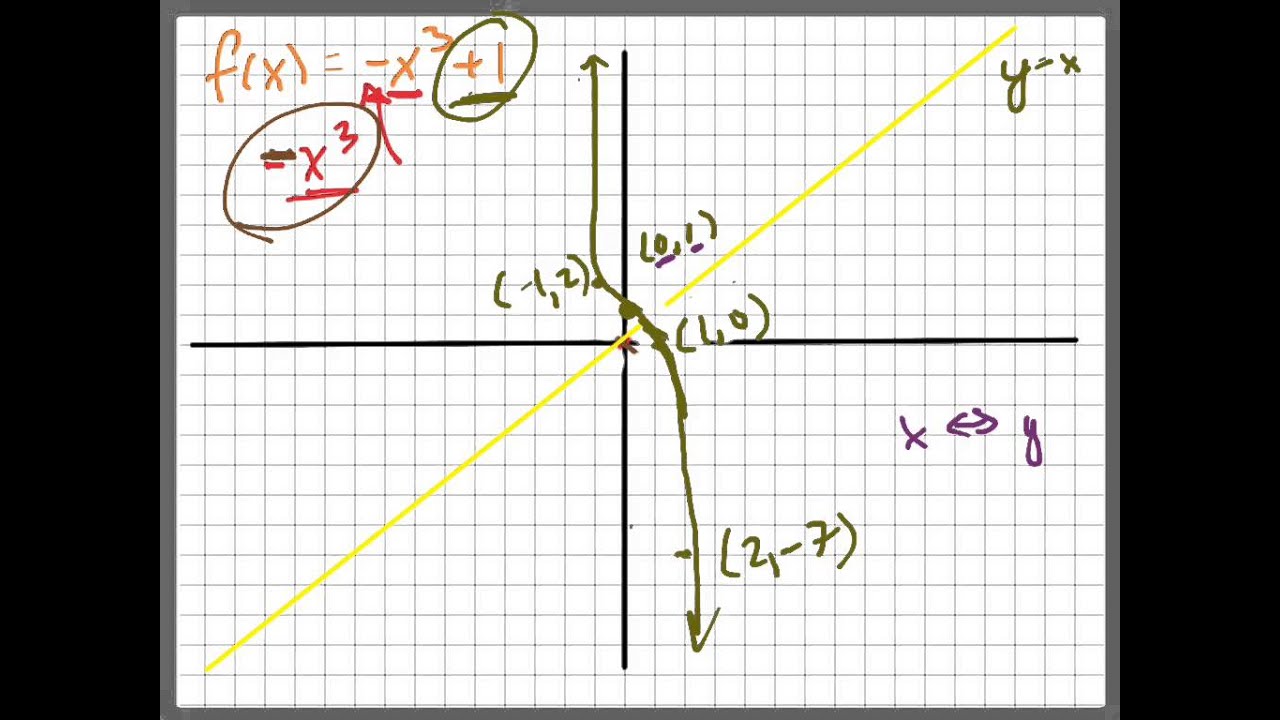



t Graph Y X 3 1 And It S Inverse Youtube



Quadratics Graphing Parabolas Sparknotes



What Does It Mean To Reflect Over The Y X Line Quora
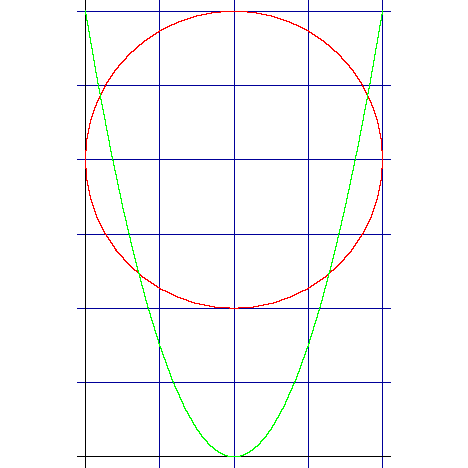



Graph Equations System Of Equations With Step By Step Math Problem Solver
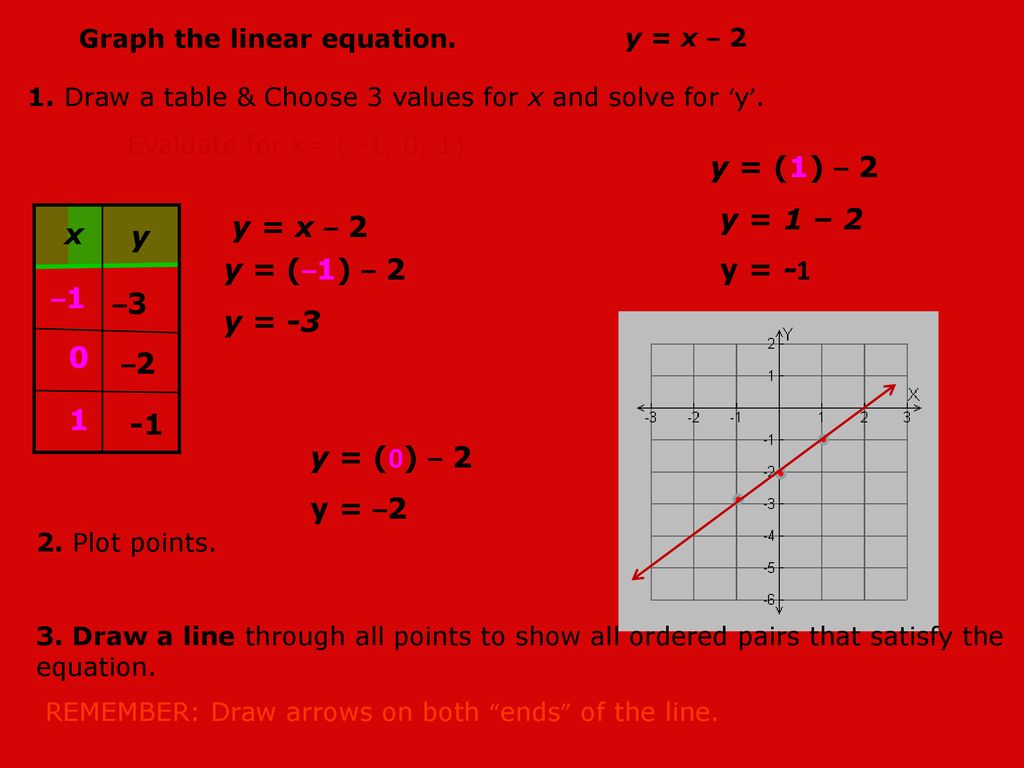



Y 1 2 Y 1 2 Y 1 Y X 2 X Y Y 1 2 Y 3 1 3 Ppt Download




1 The Region R Is The Region Bounded By The Functions Y X 3 And X 1 Y 2 Find The Volume Homeworklib



1




Solve X 1 3y 3 X 1 2y X 1 Y 6 Log X 1 Mathematics Stack Exchange
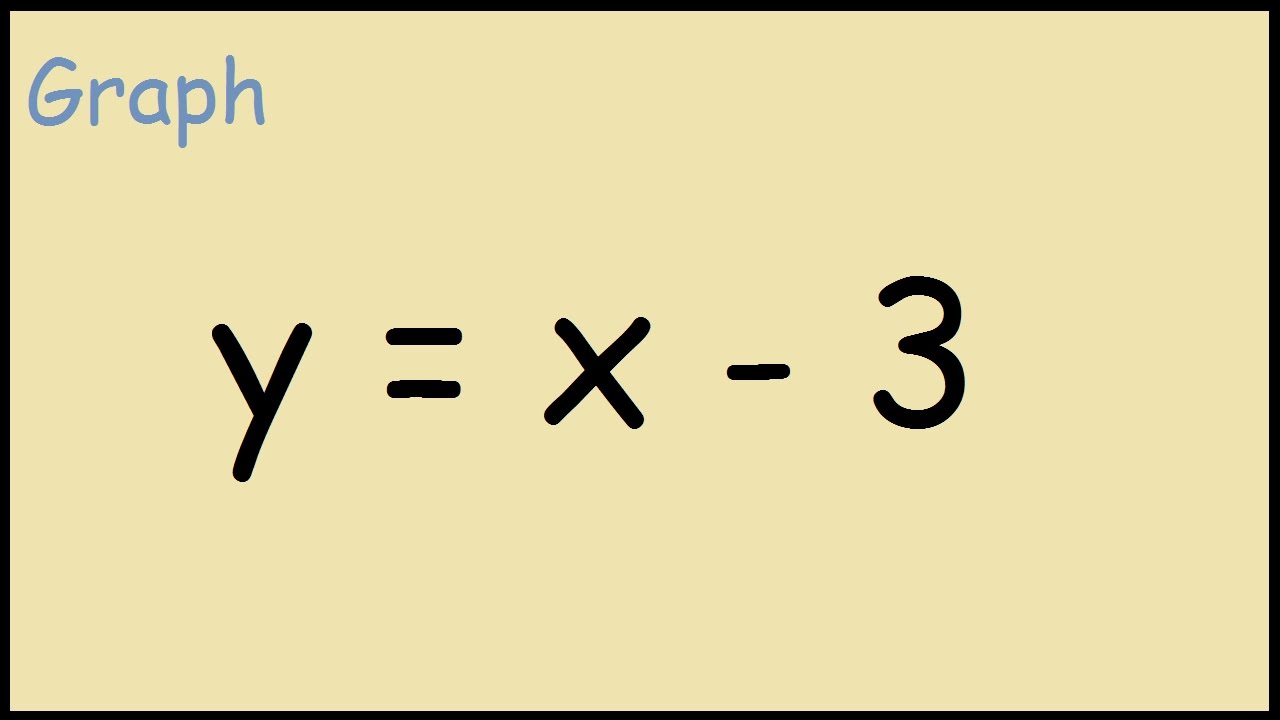



How To Graph Y X 3 Youtube




Identifying Vertical Stretch Or Shrink



Quadratics Graphing Parabolas Sparknotes




5 Derivative Of The Logarithmic Function




Graph The Linear Equation Yx 2 1 Draw



Www Yardleys Vle Com Mod Resource View Php Id




Worked Example Implicit Differentiation Video Khan Academy




Finding Linear Equations




What Does The Graph Of Math X 3 Y 3 Z 3 1 Math Look Like Quora




Below Is The Graph Of Y X 3 Translate It To Make Chegg Com



Q Tbn And9gctwl8ksal48ks9fvcggchq7ifw Mt5nzxx1 0ivsjobxia io Usqp Cau




Warm Up Solve Each Equation For X 1 Y X Y 3x 4 Ppt Video Online Download




Chapter 1 Practice Exercises




Answered 3 3x 1 34 F 33 F X 5x X2 36 Bartleby
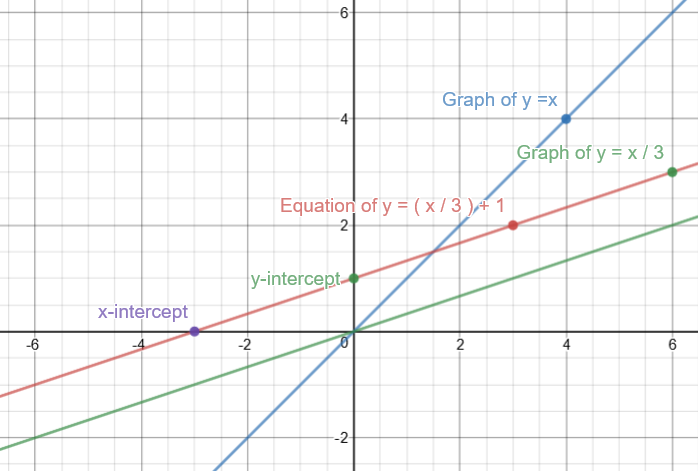



How Do You Graph Y X 3 1 Socratic




Find The Equations Of The Tangent And Normal To The Given Curves At The Indicated Points Y X3 At 1 1 Mathematics Shaalaa Com




If X 3 1 Y 2 3 5 3 1 3 Then Find The Value




If Y X 1 3 X 1 3 Then Dy Dx Is
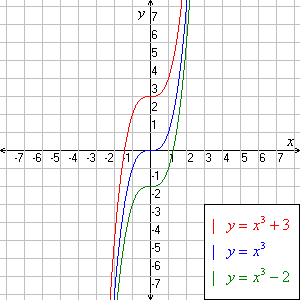



Cubic Functions




Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1
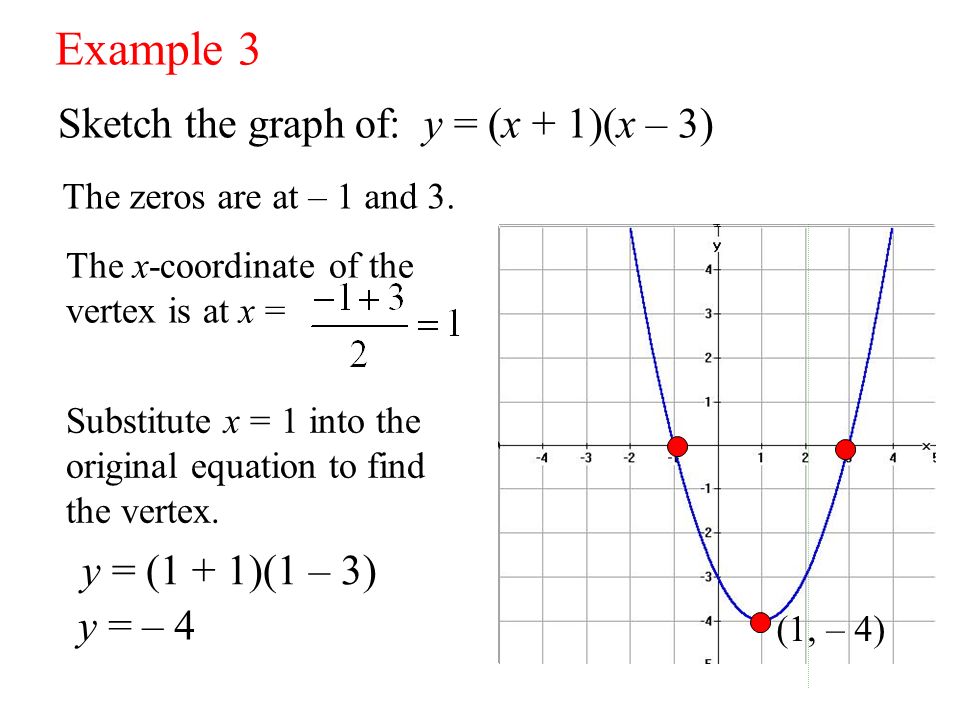



All Quadratic Equations Can Be Modeled In The Form Y A X S X T Provided A 0 If A 0 Then The Parabola Opens Up If A 0 Then The Parabola Ppt Download
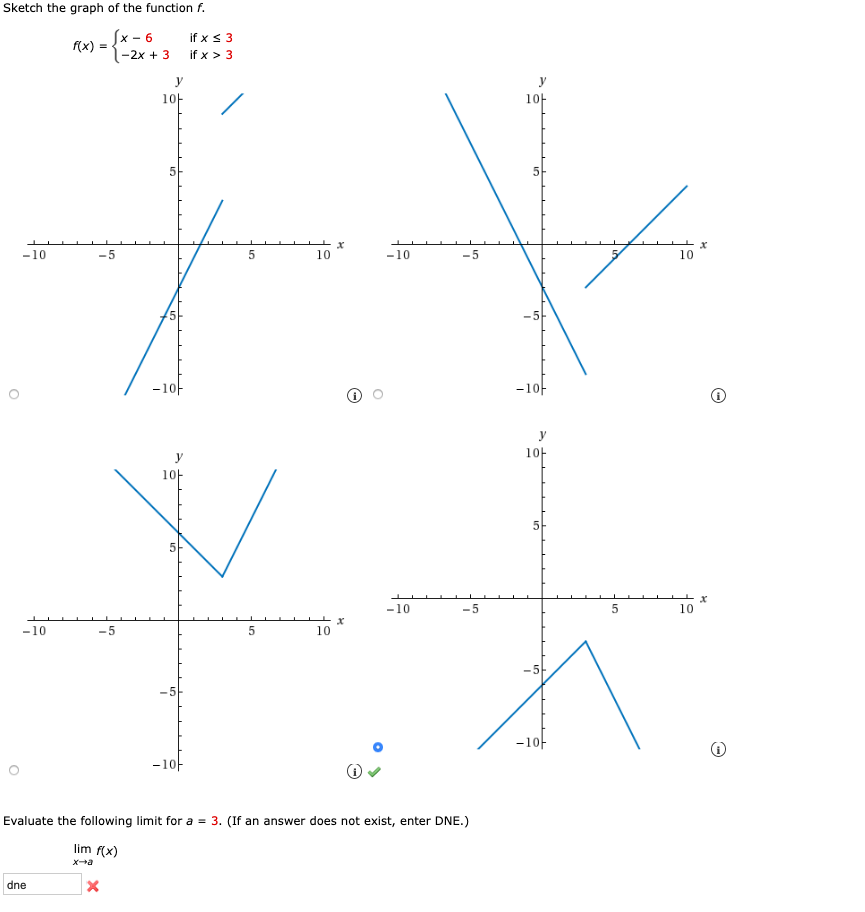



Answered Ketch The Graph Of The Function F Sx Bartleby




If Y X 1 Y Prove That X 2 Y 2 3 Dy Dx 1



Draw The Graph Of Y X 1 X 3 And Hence Solve X 2 X 6 0 Sarthaks Econnect Largest Online Education Community
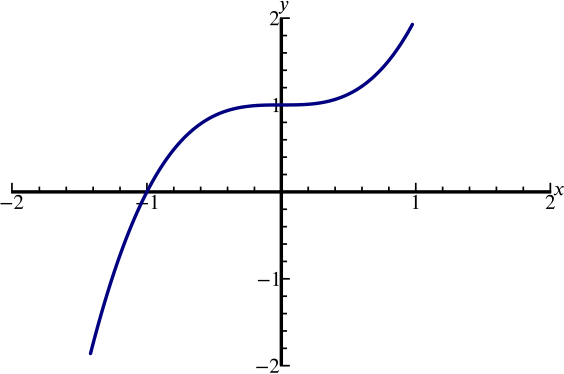



Solution Can We Sketch The Graph Y X 3 X 2 X 1 Polynomials Rational Functions Underground Mathematics



5 Derivative Of The Logarithmic Function




Using Integration Find The Area Bounded By The Curves Y X 1 And Y 3 X Mathematics Topperlearning Com 3fj45wkk



What Is The Domain And Range Of 1 X 3 Quora
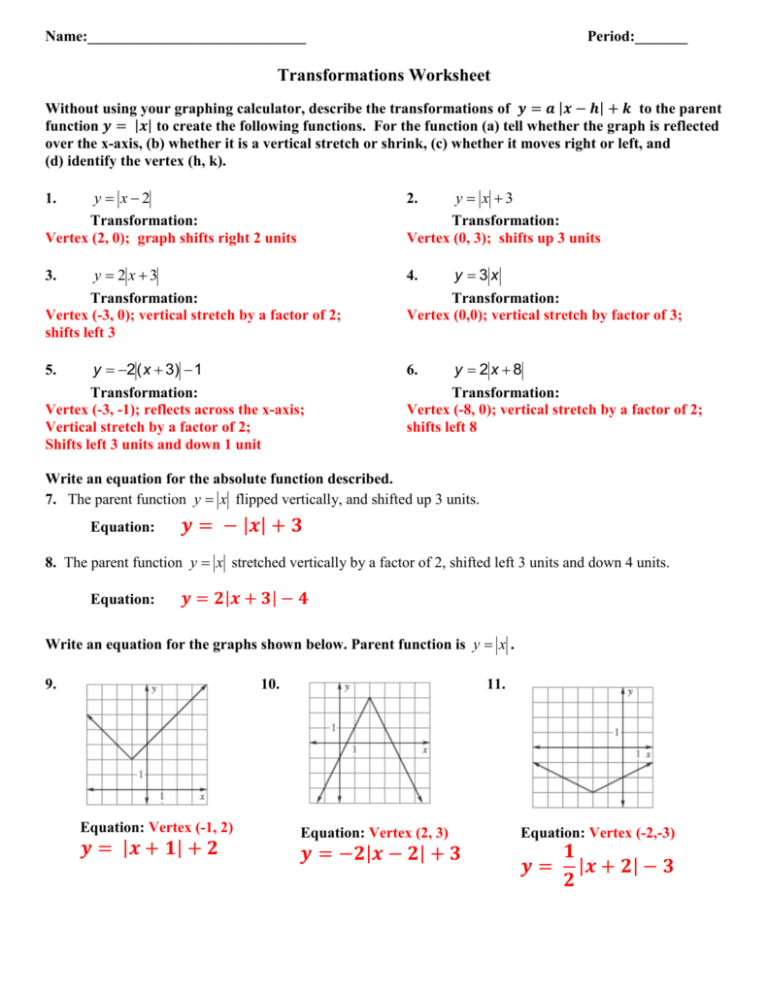



Absolute Value Transformations




Finding Linear Equations




Ex 2 1 1 If X 3 1 Y 2 3 5 3 1 3 Find X And Y



Math Spoken Here Classes Quadratic Equations 3
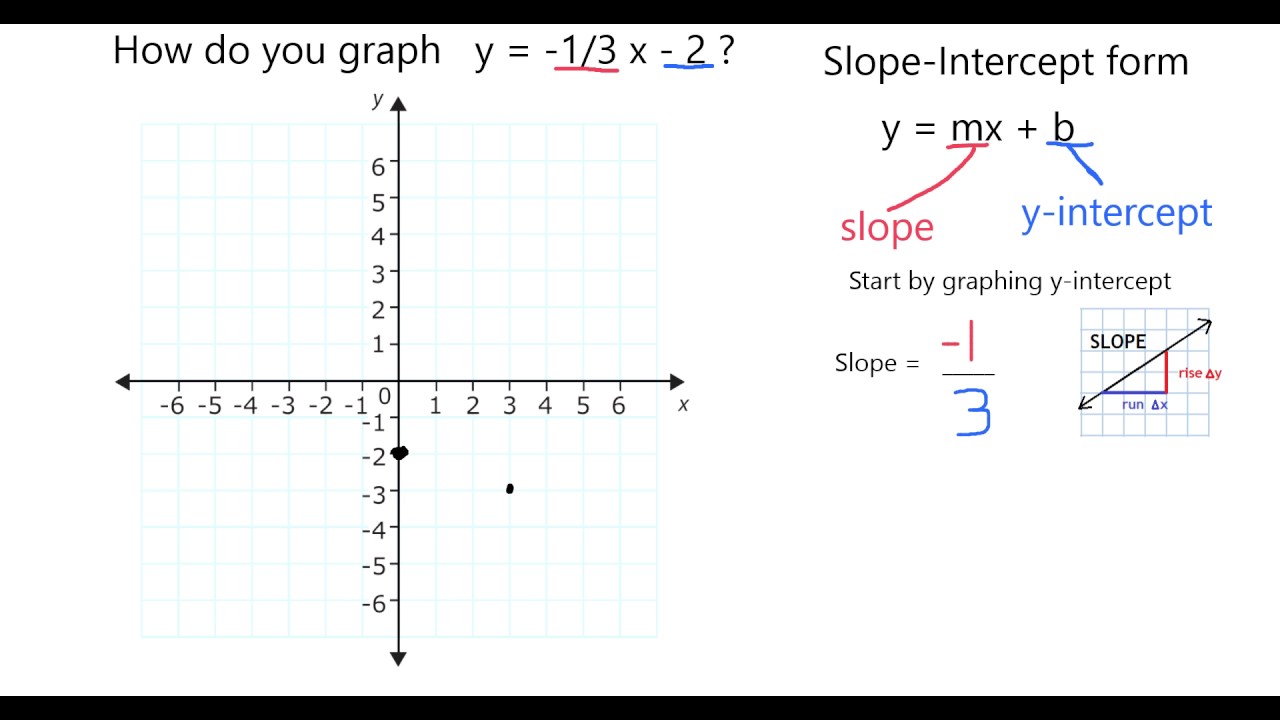



Graph Y 1 3 X 2 Youtube




Inverse Of Y X 3 X 1 Mathematics Stack Exchange



File Function X 3 1 Svg Wikimedia Commons



2
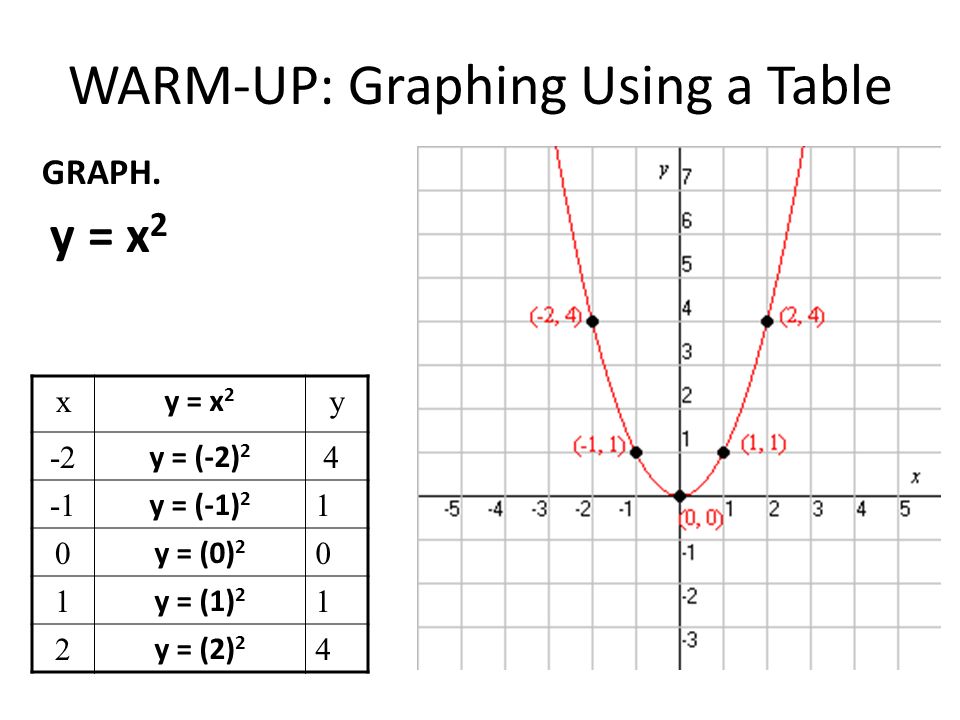



Warm Up Graphing Using A Table X Y 3x 2 Y 2 Y 3 2 2 8 Y 3 1 Y 3 0 Y 3 1 Y 3 2 2 4 Graph Y 3x Ppt Download
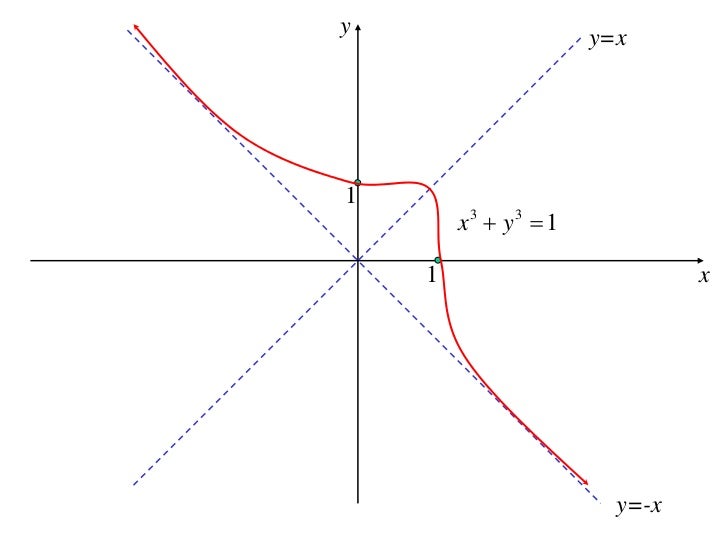



X2 T04 01 Curve Sketching Basic Features Calculus



Y X 2 Graph



For The Curve Y X 3 Given In Figure Draw I R X 3 Ii Y X 3 1 Iii Y X 3 1 Sarthaks Econnect Largest Online Education Community




Graph The Linear Equation Yx 2 1 Draw



Www Math Utah Edu Wortman 1050 Text If Pdf



0 件のコメント:
コメントを投稿